Расчет тонкостенных оболочек

Напряжения и перемещения в тонкостенных оболочках

Расчет тонкостенных оболочек основан на следующих допущениях:
а) нормальные напряжения на площадках, параллельных срединной поверхности, пренебрежимо малы по сравнению с другими компонентами напряжений;
б) совокупность точек, находящихся на нормали, проведенной к срединной поверхности до деформации, образует после деформации прямую, нормальную к деформированной срединной поверхности

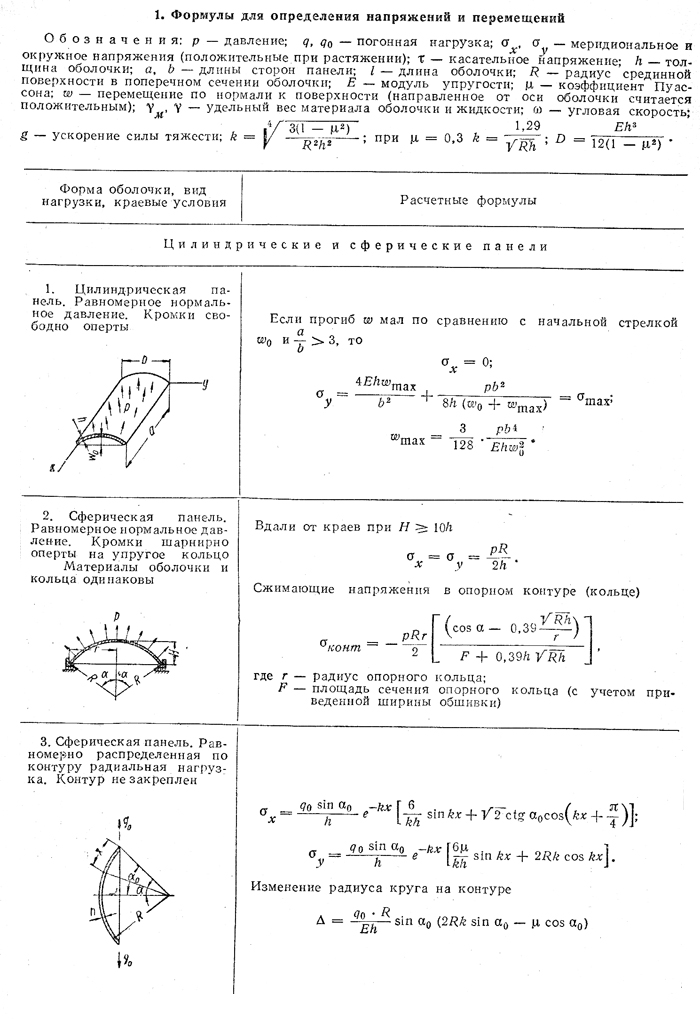
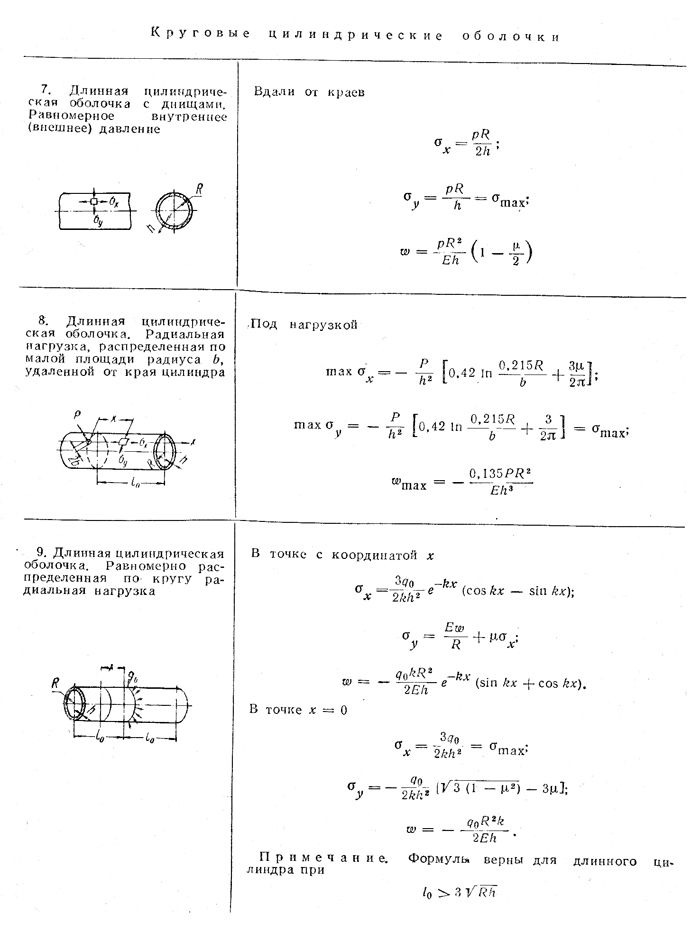
Во многих случаях можно допустить, что нормальные напряжения в нормальных сечениях оболочки распределяются равномерно по ее толщине, т. е. пренебречь изгибающими моментами, действующими в сечениях оболочки (безмоментная теория). Так, например, в зонах оболочки, достаточно удаленных от точек приложения сосредоточенных сил и моментов, от мест жесткого закрепления оболочки, от ребер усиления и вообще от мест приложения упругих и жестких связей, напряжения могут быть в обычных случаях с большой точностью определены по безмоментной теории

Изгибные напряжения носят обычно характер местного возмущения напряженного состояния и имеют существенно заметную величину лишь около мест закрепления и нагрузки.
Вследствие локальности этих напряжений их во многих случаях можно в расчет и не принимать, несмотря на то, что они достигают иногда значительных величин; их можно, например, не учитывать, если появление пластических деформаций и местное изменение формы оболочки не снижают ее несущей способности; их следует учитывать, если материал оболочки хрупкий, или если нагрузка циклическая, или такая, что снижает несущую способность оболочки

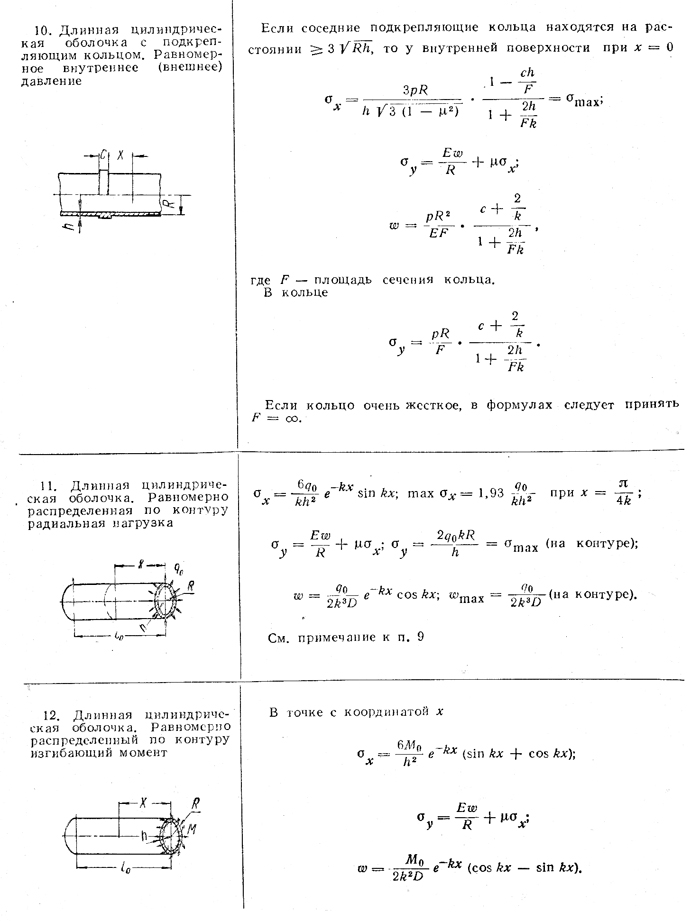
Так в цилиндрической оболочке (табл., п. 10) появление пластических деформаций в зоне жесткого кольца не снижает несущей способности оболочки, и здесь, если материал способен пластически деформироваться, местные изгибные напряжения могут в расчет не приниматься. В этом случае достаточно ограничиться только определением общих напряжений по безмоментной теории и установить по ним условие прочности

То же самое можно сказать и о температурных напряжениях. Эти напряжения следует учитывать в случае, когда материал оболочки хрупкий; если же материал обладает пластическими свойствами, учет влияния температуры производится только путем соответствующего снижения механических характеристик материала (предел текучести и прочности) без учета температурных напряжений

Для оболочки, имеющей форму тела вращения, при симметричном нагружении меридиональное напряжение σ_х может быть найдено из условия равновесия части оболочки, отсеченной нормальным круговым сечением, а окружное напряжение σ_у — из уравнения Лапласа