Примеры расчетного определения размеров пружин

Расчет пружины сжатия

Исходные данные
F₁ = 20H; F₂ = 80H; D₁ = 10 ÷ 12 мм; v _max = 5 м/с; N _F ≥ 1•10⁷

Пользуясь таблицами «Параметры пружин» (http://razvitie-pu.ru/?page_id=4672) убеждаемся, что при заданной выносливости пружину следует отнести к классу I

По формуле (2), пользуясь интервалом значений δ от 0,05 до 0,25 формула (1), находим граничные значения силы F ₃

В интервале от 84 до 107 Н (ГОСТ 13766) пружин класса I, разряда 1 имеются следующие силы F₃; 85; 90; 95; 100 и 106 Н.
Исходя из заданных размеров диаметра и стремления обеспечить наибольшую критическую скорость, останавливаемся на витке со следующими данными (номер позиции 355): F₃ = 106 Н; d = 1,80 мм; D₁ = 12 мм; с₁ = 97,05 Н/мм; s’₃ = 1,092 мм

Учитывая, что для пружин класса I норма напряжений τ ₃ = 0,З R_m, для найденного диаметра проволоки из углеродистой холоднотянутой стали расчетное напряжение τ ₃ = 0,3 • 2100 = 630 Н/мм²

Принадлежность к классу I проверяем путем определения отношения v_max /v_k для чего предварительно определяем критическую скорость по формуле (5) при δ = 0,25:

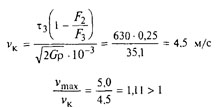
Полученная величина свидетельствует о наличии соударения витков в данной пружине, и, следовательно, требуемая выносливость может быть не обеспечена. При меньших значениях силы F₃ отношение v_max / v_к будет еще больше отличаться от единицы и указывать на еще большую интенсивность соударения витков

Используем пружины класса II. Заданному наружному диаметру и найденным выше силам F₃ соответствует виток со следующими данными по ГОСТ 13770(позиция 303):
F₃ =95,0 Н; d = 1,4 мм; D₁ =11,5 мм; с₁ = 36,58 Н/мм; s’ ₃ = 2,597 мм.
Учитывая норму напряжений для пружин класса τ ₃ = 0,5 R_m, находим τ ₃ = 0,5•2300 =1150 Н/мм². По формуле (2) вычисляем δ = 1 — F₂ / F₃ = 1 — 80/95 = 0,16 и находим v_k и v_max / v_k , с помощью которых определяем принадлежность пружин ко II классу:

Полученная величина указывает на отсутствие соударения витков, и, следовательно, выбранная пружина удовлетворяет заданным условиям, но так как пружины класса II относятся к разряду ограниченной выносливости, то следует учитывать комплектацию машины запасными пружинами с учетом опытных данных.
По формуле (6) находим жесткость пружины

Число рабочих витков пружины определяем по формуле (7)

Уточненная жесткость имеет значение

При полутора нерабочих витках полно< число витков находим по формуле (8):
n₁ = n + n₂ = 18,5 + 1,5 = 20
По формуле (9) определяем средний диаметр пружины
D = 11,5 — 1,40 = 10,1 мм
Деформации, длины и шаг пружины определяем по формулам (11) — (18)

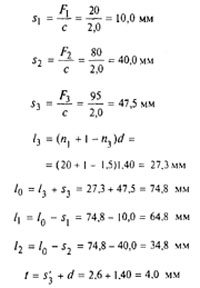
На этом определение размеров пружины и габарита узла (размер l ₁) заканчивается.
Следует отметить, что некоторое увеличение выносливости может быть достигнуто при использовании пружины с большей величиной силы F ₃, чем найденная в настоящем примере

С целью выяснения габаритов, занимаемых такой пружиной, проделаем добавочный анализ, остановимся, например, на нитке со следующими данными по ГОСТ 13770 (позиция 313):
F₃ = 106 Н; d = 1,4 мм; D₁ = 10,5 мм; с₁ = 50,01 Н/мм; s’ ₃ = 2,119 мм

Находим τ ₃ = 1150 Н/мм² и производим расчет в той же последовательности:

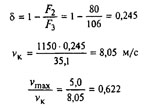
У этой пружины создается большой запас на несоударяемость витков.
Далее в рассмотренном ранее порядке находим n = 50,01 : 2,0 = 25,01 ≈ 25,0
Уточненная жесткость с = 50,01 : 25,0 = 2,0 Н/мм;
n 1 = 25,0 + 1,5 = 26,5
D = 10,5 — 1,4 = 9,1 мм
s ₁ = 20 : 2,0 = 10 мм
s ₂ = 80 : 2,0 = 40 мм
s ₃ = 106 : 2,0 = 53 мм
l ₃ = (26,5 + 1 — 1,5)1,4 = 36,4 мм
l ₀ = 36,4 + 53 = 89,4 мм
l ₁ = 89,4 — 10 = 79,4 мм
l ₂ = 89,4 — 40 = 49,4 мм
t = 2,1 + 1,4 = 3,5 мм

Вывод: применение пружины с более высокой силой F ₃ хотя и привело к большему запасу на несоударяемость витков, но оно сопровождается увеличением габарита узла (размер l ₁) на 15,3 мм. Можно показать, что если выбрать виток с большим диаметром, например D ₁ = 16 мм (ГОСТ 13770, номер позиции 314) — потребуется расширить узел по диаметру, но при этом соответственно уменьшится размер l ₁

Расчет пружины сжатия (2 вариант)

Исходные данные
F₁ = 100H; F₂ = 250H; h = 100 мм; D₁ = 15 ÷ 25 мм; v _max = 10 м/с

Независимо от заданной выносливости на основании формулы (5) можно убедиться, что при значениях δ , меньших 0,25 [формула (1)], все одножильные пружины, нагружаемые со скоростью v _max более 9,4 м/с, относятся к III классу.
По формуле (2) с учетом диапазона значений δ для пружин класса III от 0,1 до 0,4 [формула (1)] находим границы сил F ₃
F ₃ = F ₂ : (1 — 0,1)…F ₂ : (1 — 0,4) = 250 : 0,9…250 : 0,6 = 278…417 Н

Верхние значения силы F₃ не могут быть получены из числа одножильных конструкций, поэтому, учитывая коэффициенты δ = 0,15…0,40 [формула (1)] для трехжильных пружин, устанавливаем новые пределы F₃, по формуле (2):
F₃ = 294…417 Н
Для указанного интервала в ГОСТе 13774 имеются витки со следующими силами F₃: 300; 315; 335; 375 и 400.
Исходя из заданных размеров диаметра и наименьших габаритов узла, предварительно останавливаемся на витке со следующими данными (номер позиции 252):
F₃ = 300 Н; d = 1,4 мм; d ₁ = 3,10 мм; D ₁ = 17 мм; с ₁ = 50,93 Н/мм; s’ ₃ = 5,900 мм

Согласно ГОСТ 13764 для пружин класса III τ ₃ = 0,6 R _m. Используя ГОСТ 9389, определяем напряжение для найденного диаметра проволоки
τ ₃ = 0,6 х 2300 = 1380 МПа
Принадлежность к классу проверяем путем определения величины отношения v _max / v _k, для чего предварительно находим δ и критическую скорость по формулам (1), (2), (5а)

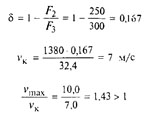
Полученное неравенство свидетельствует о наличии соударения витков и о принадлежности пружины к классу III.
По формуле (6) находим жесткость

Число рабочих витков пружины вычисляют по формуле (7)

Уточненная жесткость

Полное число витков находят по формуле (8):
n ₁ = n + 1,5 = 34,0 + 1,5 = 35,5
По формуле (9а) определяют средний диаметр пружины
D = D ₁ — d ₁ = 17 — 3,10 = 13,90 мм
Деформации, длины и шаг пружины находят по формулам (10а)…(18а)

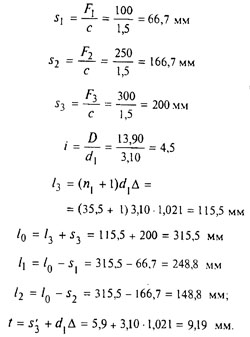
Проанализируем пружины, соответствующие трем ближайшим значениям F₃, взятым из ГОСТа 13774 (пружины класса III, разряда 1).
Вычисления показывают, что для трех соседних сил F₃ образуется шесть размеров пружин, удовлетворяющих требованиям по величине наружного диаметра. Сведения о таких пружинах приведены ниже

F 3, H	300	300	315	315	335	335
d, мм	1,4	1,6	1,4	1,6	1,4	1,6
d 1,мм	3,10	3,50	3,10	3,50	3,10	3,50
D 1, мм	17,0	24,0	16,0	22,0	15,0	21,0
v max / v k	1,43	1,50	1,16	1,21	0,942	0,984
l 0, мм	317,0	273,9	355,1	309,0	405,1	337,0
l 1, мм	250,4	207,2	288,4	242,3	338,4	270,3
l 2, мм	150,4	107,2	188,4	142,3	238,4	170,3
n 1	36,0	20,0	44,5	27,0	56,0	31,0
V, мм3	57000	93000	58000	92000	60000	93000

Из этих данных следует, что с возрастанием F₃ уменьшается отношение v _max / v _k и, в частности может быть устранено соударение витков, но вместе с этим возрастают габариты по размерам l ₁.
С возрастанием диаметров пружин габариты по размерам l ₁ уменьшаются, однако существенно возрастают объемы пространств, занимаемых пружинами

Следует отметить, что если бы для рассматриваемого примера, в соответствии с требованиями распространенных классификаций, была выбрана пружина класса I, то при одинаковом диаметре гнезда (D ₁ ≈ 18 мм) даже самая экономная из них потребовала бы длину гнезда l ₁ = 546 мм, т. е. в 2,2 раза больше, чем рассмотренная выше. При этом она была бы в 11,5 раза тяжелее и, вследствие малой критической скорости (v _k = 0,7 м/с), практически неработоспособной при заданной скорости нагружения 10 м/с

Расчет пружины растяжения

Исходные данные
F₁ = 250 H; F₂ = 800 H; h = 100 мм; D₁ = 28 ÷ 32 мм; v _max = 5 м/с; N _F ≥ 1•10⁵

На основании ГОСТа — пружина относится к II классу

В интервале сил 842—889 Н по ГОСТ 13770 для пружин класса II, разряда 1 (номер пружины 494) имеется виток со следующими параметрами:
F ₃ = 850 H, D ₁ = 30 мм, d = 4,5 мм, с ₁ = 242,2 Н/мм, s’ ₃ = 3,510 мм

По заданным параметрам с помощью формулы (6) определяем жесткость пружины

Число рабочих витков находим по формуле (7):

Деформации и длины пружины вычисляют по формулам

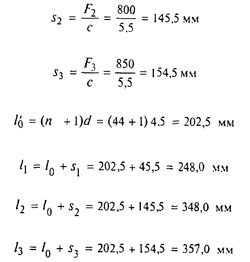
Размер l ₂ с учетом конструкций зацепов определяет длину гнезда для размещения пружины растяжения в узле.
Размер l ₃ с учетом конструкций зацепов ограничивает деформацию пружины растяжения при заневоливании

Трехжильные пружины (угол свивки 24°)

Жесткость

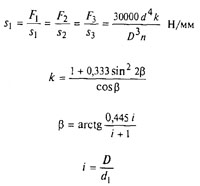
Напряжение

Полученные значения жесткости должны совпадать с вычисленными по формуле (6).
Полученные значения напряжений должны совпадать с указанными в ГОСТ 13764 для соответствующих разрядов с отклонениями не более ± 10 %