Развертки поверхностей бункеров

Бункером называется специальный резервуар, предназначенный для вмещения и перегрузки сыпучих материалов. Бункеры бывают разнообразной формы. Наиболее распространенные приведены на рис. 1 и 2. Форма бункеров на рис.1, а, б, в, г представляет собой сочетание из форм призмы и пирамид прямой или наклонной.

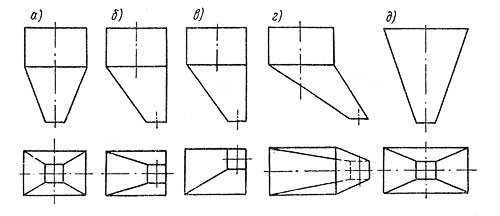
Рисунок 1

На рис.1, д изображен пирамидальный бункер. Форма бункеров на рис.2, а, б, в — образована сочетанием цилиндра и конуса — кругового (рис.2, а) и эллиптического (рис.2, б, в)

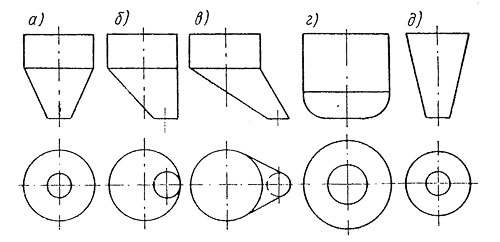
Рисунок 2

На рис.2, г — сочетанием цилиндра и сферы; на рис.2, д изображен конический бункер.

В качестве примера для построения развертки на рис. 3, а дан бункер, форма которого представляет собой прямую усеченную прямоугольную пирамиду.

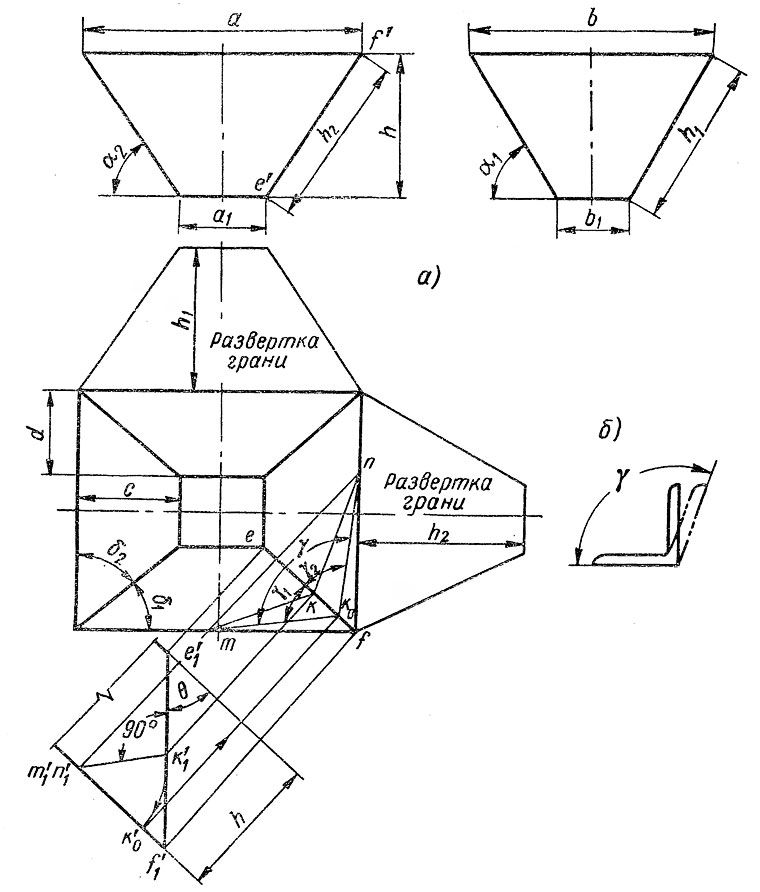
Рисунок 3

Заданными величинами являются размеры отверстий a, a1 и b, b1 и высота пирамиды h.
Для хорошего опорожнения бункера необходимо, чтобы наименьший угол наклона стенки (грани) бункера к горизонту, в данном случае угол α2, был больше на 5 — 10º угла естественного откоса сыпучего материала в условиях покоя. Чтобы материал не зависал на ребрах бункера, следует определить угол наклона ребер к горизонту θ. Он должен быть несколько больше угла трения материала о стенку бункера.

Для определения величины этого угла, который, очевидно, будет всегда меньше углов α1 ;и α2, построена вспомогательная проекция бункера, на которой одно из ребер бункера — ребро EF изобразилось в натуральную величину. Угол наклона θ этого ребра к горизонтальной плоскости и будет искомым. Как видно из чертежа, этот угол может быть рассчитан и аналитически по формулам 1.

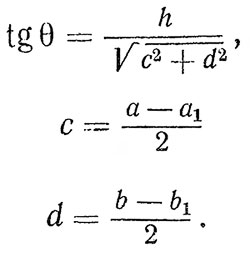
Формула 1

Обычно размеры бункера таковы, что его поверхность не может быть выполнена из одного листа, поэтому для его изготовления определяют форму и размеры каждой грани, а затем их соединяют при помощи сварки.

Боковые грани бункера представляют собой равнобочные трапеции. Их основания заданы и соответственно равны a, a1, b, b1, а их высоты h1 и h2 определяются на фронтальной и профильной проекциях. Для изготовления каркаса бункеров большой ёмкости требуется определение угла γ, например, для размалковки угловой стали, из которой выполняется каркас бункера, см.рис. 3, б.

Этот угол является линейным углом, измеряющим двугранный угол между двумя смежными гранями пирамиды. Он получится, если пересечь грани плоскостью, перпендикулярной их ребру. Его натуральная величина определена на рис. 3 следующим образом. Двугранный угол при ребре EF пересечен плоскостью, перпендикулярной к этому ребру и проходящей через произвольную точку К ребра. Тогда в сечении получится треугольник MNK, причем угол при вершине Ки будет искомым.

На вспомогательной проекции бункера этот треугольник изображен прямой (m’₁, n’₁) k’₁, а треугольник mnk является его горизонтальной проекцией. Для определения натуральной величины угла MKN = γ достаточно расположить прямую (m’₁ n’₁) k’1 параллельно горизонтальной плоскости, т.е. поставить ее в положение (m’1 n’1) k’0. Тогда угол mk₀n и будет искомым.

Угол γ может быть рассчитан аналитически по формуле: γ = γ1 + γ2, где углы γ1 и γ2, в свою очередь, определяются из зависимости:

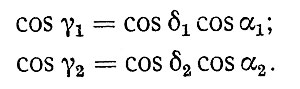
Формула 2

На рис. 4 изображен бункер, поверхность которого представляет собой сочетание кругового цилиндра и эллиптического конуса.

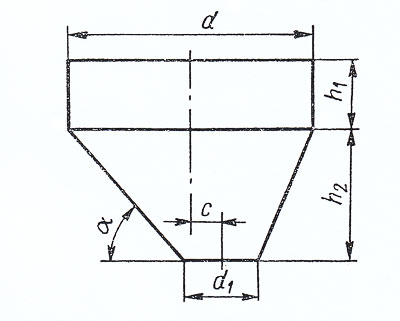
Рисунок 4

Наименьший из углов наклона его образующих к горизонту, в данном случае угол α, должен быть на 5 — 10º больше угла естественного откоса сыпучего материала в состоянии покоя.

Развертка верхней цилиндрической части бункера будет представлять собой прямоугольник размерами πD х h1. Развертка нижней части бункера — усеченного эллиптического конуса с круговым основанием — может быть построена при доступной (см. рис. 4, а) или недоступной (см. рис. 4, б) вершине конуса.

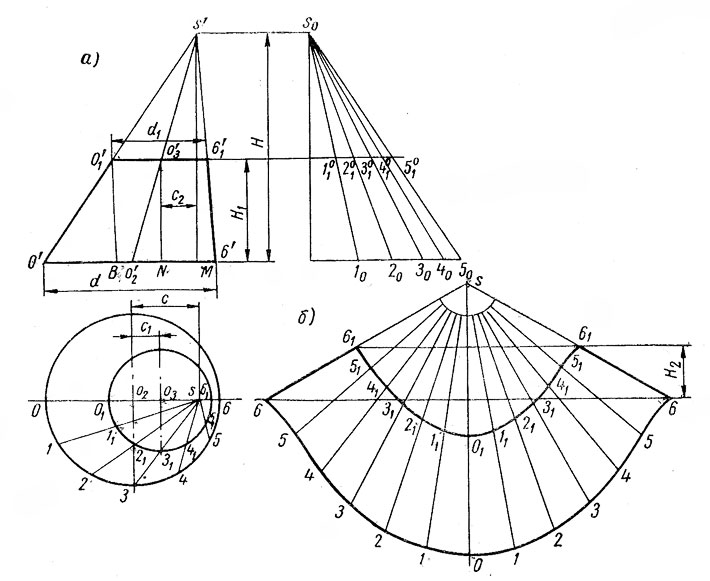
Рисунок 4a

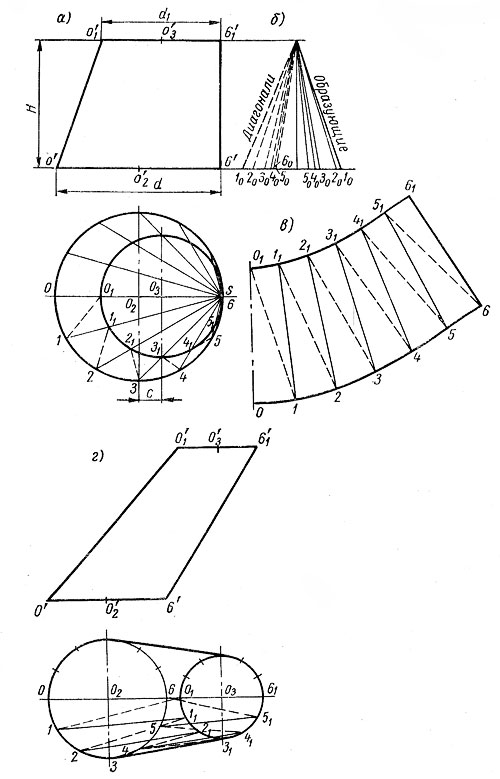
Рисунок 4б

Однако следует заметить, что ввиду больших погрешностей, которые получаются в последнем случае построения развертки, лучше пойти на уменьшение масштаба (но не менее 1:10) и выполнить, если возможно, построение развертки при доступной вершине конуса.

Натуральные длины образующих могут быть определены аналитически по формуле 1 и таблице (см. раздел «переход круга в прямоугольник»).

На рис. 5 приведен бункер корытообразной формы — параболический бункер.

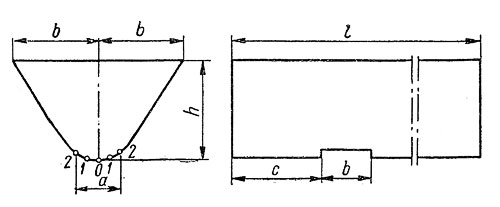
Рисунок 5

Такие бункеры изготавливаются из стальных листов и применяются для кратковременного хранений сыпучих материалов при постепенном их расходовании. Выгрузка материала производится через люки, расположенные в донной части корыта. Один из таких люков изображен на рис. 5. Форма торцовой стенки имеет вид параболы, уравнение которой в функциональной зависимости х/b имеет вид:

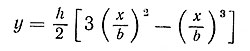
Формула 3

Пользуясь вышеприведенным уравнением, можно построить контур торцовой стенки для раскроя материала. Для облегчения вычислительных операций ниже приводится таблица отношений y/h в зависимости от значений x/b:

x/b	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
y/h	0,014	0,056	0,126	0,208	0,312	0,432	0,563	0,704	0,851	1,000

По данным этой таблицы и построен контур стенки на рис.6

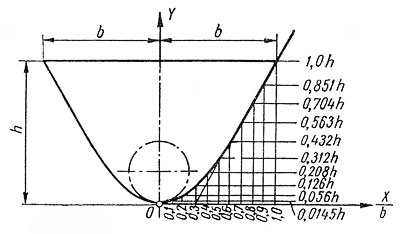
Рисунок 6

На рис.7 дан графический прием построения очертания стенки по заданным b и h.

Рисунок 7

Уравнение контура стенки может быть представлено в виде разности двух функций
(ф-ла 4). Уравнение (ф-ла 5) — уравнение параболы второго порядка, а уравнение (ф-ла 6) представляет собой уравнение кубической параболы. Вершины обеих парабол расположены в начале координат.

Для построения одной ветви параболы 2-го порядка определяют ординату её крайней точки (точка А): при x = b y’a = 3/2 h. Затем отрезки ОВ = b и ВА = 3/2 h делят на одинаковое число равных частей, например на четыре части, и нумеруют точки согласно рис. 7.

Вершину 0 соединяют с точками делений отрезка АВ, а из точек делений отрезка ОВ проводят прямые, параллельные оси OY. Пересечением одинаково занумерованных лучей определяют ряд точек параболы.

Для удобства построения правую ветвь кубической параболы располагают ниже оси ОХ, т.е. строят её по уравнению y’’ = — h/2(x/b)3. Вначале так же определяют ординату её крайней точки С при x = b; y’’ = — h/2. Затем на отрезке ВС = h/2, как на диаметре, строят полуокружность и этот отрезок делят на то же число равных частей, на которое ранее был разделен отрезок ОВ, т.е. на четыре равных части. Точки делений I, II и III переносят на полуокружность, проводя дуги из цента В. Из полученных точек I1, II1 и III1 опускают перпендикуляры на ВС и точки 1, 2, и 3 соединяют с точкой О. В пересечении этих лучей с прямыми, проведенными через точки 1, 2 и 3 отрезка ОВ параллельно оси OY, получают точки кубической параболы.

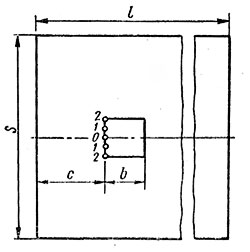
Рисунок 8

По разности (алгебраической) ординат построенных двух кривых строят искомую кривую. Вторая ветвь её строится аналогичным образом. Для построений развертки боковой поверхности бункера (рис. 8), которая будет представлять прямоугольник размером s х l, необходимо определить s, т.е. длину параболы. Она может быть определена по формуле s = kb.

Ниже приведены значения коэффициента k для наиболее употребительных отношений h/b.

h/b	2/3	3/4	7/8	1/1	6/5	4/3	3/2
k	2,4599	2,5661	2,7330	2,9144	3,2226	3,4381	3,7163

Длина кривой s может быть приблизительно построена графически, путем замены небольших её отрезков прямыми. Для уменьшения ошибки следует брать отрезки кривой, мало отличающиеся по длине от стягивающих хорд.

Итак, имея длину бункера l и определив размер s, строят развертку его боковой поверхности (рис.8). На развертке нанесено отверстие одного из разгрузочных люков, изображенного на рис. 5. Его построение ясно из чертежа.

Коэффициенты трения и угол естественного откоса некоторых сыпучих материалов

Материал	Угол естественного откоса, °	Коэффициент трения				Плотность, т/мsup>3	Объемная масса в рыхлом насыпном состоянии, т/м3	Размер частиц, мм
		внутренний	по стали	по дереву	по резине
Гипс строительный	40	0,58 — 0,82	0,61 — 0,78		0,70 — 0,82	2,5	0,8 — 0,9	0,02
Глина порошковая	35	0,84 — 1,00	0,75 — 1,00			1,6 — 2,0	1,0 — 1,5	0,1
Известь порошковая	43	0,56 — 0,7	0,35	0,4		1,3 — 1,4	0,5 — 0,7	0,1
Известняк молотый		0,57 — 1,26	0,56 — 1,00	0,7	0,66	2,73	0,9 — 1,2	0,49
Зола сухая	40 — 45	0,84 — 1,2	0,60 — 0,85	1,0		2,5 — 3,0	0,6 — 0,8	0,04
Кремний порошковый	35 — 45	0,57 — 0,84	0,32 — 0,84		0,46 — 0,56	2,65	1,15	0,25
Минеральный порошок						2,53	0,95 — 1,2	0,05
Мел порошкообразный	45	0,81				1,8 — 2,7	0,95 — 1,2	0,3
Цемент	40 — 50	0,50 — 0,84	0,30 — 0,65	0,3 — 0,4	0,61	2,8 — 3,2	0,8 — 1,2	max 0,09
Сода кальционированная	43 — 45	0,71 — 1,02	0,3 — 0,7	0,48	0,44 — 0,68	2,53	0,55 — 0,80	max 0,04
Керамзит	35 — 40						0,25 — 1,0	0,1 — 2,0
Песок	40 — 45	0,8	0,8		0,56	2,5 — 2,9	1,5 — 1,7	0,1 — 1,0
Сухая цементно-песчаная смесь	40 — 50							0,02 — 2,5

По материалам:
«Технические развертки изделий из листового металла» Н.Н. Высоцкая 1968 г. «Машиностроение»