Ременные передачи

Служат для передачи вращения между двумя шкивами при помощи гибкой связи — ремня

Достоинства: возможность пробуксовки ремня при ударах нагрузки, что спасает звенья механизмов от поломок; бесшумная работа на высоких и сверхвысоких скоростях; простота конструкции передачи.
Недостатки: большие габариты передачи; нестабильное передаточное отношение в связи со скольжением ремня

Конструктивные типы ремней

Ремни подразделяется на два основных вида: плоские и клиновые.
Плоские ремни бывает:
а) кожаные — лучший тип ремней;
б) прорезиненные — основной наиболее распространенный тип;
в) текстильные тканые — шерстяные, хлопчатобумажные и из синтетических материалов. Эти ремни чаще всего цельнотканые без сшивки

Клиновые ремни стандартизованы по сечению и длине, не имеют сшивки и состоят из центрального армирующего слоя, окруженного резиновым сердечником в форме трапеции, который защищен снаружи слоями прорезиненной ленты. Эти ремни работают боковыми гранями, угол между которыми составляет около 40°, поэтому трапецеидальные канавки на шкивах должны обеспечить значительный радиальный зазор между ремнем и дном канавки. Число ремней на шкиве колеблется от 1 до 8, но обычно от 1 до 4. По размеру сечения таблицами ГОСТ предусматриваются следующие типы ремней: О, А, Б, В, Г, Д, Е. Для каждого типа (сечения ремня) в таблицах указываются: размеры сечения, площадь сечения, длина, минимальный диаметр шкива, допускаемая нагрузка и вес

Сравнение плоских и клиновых ремней по тяговой способности

Сила трения на поверхности плоского ремня: F _n = P f

Сила трения на поверхностях трения клинового ремня:

при α = 20°, sinα = 0,34, F_к ≈ 3Pf

Теоретически тяговая способность клинового ремня при том же усилии натяжения в 3 раза больше, чем у плоского.
Однако относительная прочность клинового ремня по сравнению с плоским несколько меньше (в нем меньше слоев армирующей ткани), поэтому практически тяговая способность клинового ремня приблизительно в два раза выше, чем у плоского. Это свидетельство в пользу клиновых ремней послужило основанием для их широкого распространения, в особенности в последнее время

Устройства для натяжения ремня

Чтобы ременная передача могла передавать полезное окружное усилие, ремень должен быть натянут расчетным усилием S₀. Для натяжения ремней применяются следующие способы:
натяжение приводным мотором при помощи винтовых устройств;
натяжение натяжным шкивом при помощи постоянного усилия, создаваемого пружиной, или грузом противовеса;
упругое натяжение за счет укороченной против расчетной длины ремня.
Последний способ не дает стабильного натяжения, поэтому применяется редко

Расчетные геометрические зависимости в ременной передаче

α₁, α₂ — углы обхвата;
R₁, R₂ — радиусы шкивов;
A — межцентровое расстояние

α₁ = 180° — γ;    α₂ = 180° + γ

Свободная теоретическая длина ремня

Диаметр малого шкива по опытной формуле Саверина

N — мощность в кВт;
n — число оборотов в минуту.
D₂ = D₁i, уточненно D₂ =D₁ i(1 —ξ ), где ξ — коэффициент упругого скольжения ремня.
Диаметры шкивов округляются до ближайшего значения по ГОСТ

Упругое скольжение ремня

По формуле Эйлера для трения гибких тел натяжение набегающей ветви ремня S₁ больше, чем натяжение сбегающей S₂:

Здесь: α — угол обхвата ремня;
β — угол упругого скольжения ремня;
f — коэффициент трения ремня по шкиву;
l — основание натуральных логарифмов

Так как натяжение ветвей ремня неодинаково, то и относительное удлинение их по закону Гука также будет неодинаковым. На дуге α эти удлинения выравниваются, что может иметь место лишь при условии упругого скольжения ремня, величина дуги α зависит от передаваемой нагрузки. Если нагрузку все время увеличивать, то в пределе дуга достигнет дуги β. Физически это будет соответствовать полному буксованию ремня, что совершенно недопустимо. Относительное удлинение ветвей ремня:

Относительное упругое скольжения ремня:

Упругое скольжение ремня под нагрузкой вполне закономерно, оно обычно не превышает 0,02 (2%); если передачу перегрузить, то упругое скольжение переходит в недопустимое буксование

Силы, действующие в ременной передаче

Окружное усилие

Усилие предварительного натяжения ветвей ремня — S₀
Усилие натяжения ветвей ремня в работе. На основе равновесия гибкой нити: S₁ — S₂ = Р

Теорема Понселе:   Сумма усилий натяжения ветвей ремня в состоянии покоя и движения под нагрузкой есть величина постоянная: S₁ + S₂ = 2S₀

Следствие теоремы Понселе:   При переходе от состояния покоя к состоянию работы под нагрузкой усилие набегающей ветви увеличивается на величину половины окружного усилия, усилие сбегающей — на столько же уменьшается

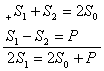
Нагрузка на валы и подшипники:

Коэффициент тяги и кривые скольжения ремня

Коэффициентом тяги называется отношение полезного окружного усилия к полному усилию натяжения ветвей ремня.
По физическому смыслу коэффициент тяги характеризует степень загрузки передачи:

Зависимость между коэффициентом тяги и коэффициентом упругого скольжения ремня, выраженная графически, носит название кривых скольжения ремня. Оптимальный режим работы ремня при высшем значении КПД должен находиться в зоне упругого скольжения. На основании кривых скольжения определяются допускаемые напряжения в ремне

Напряжения в ремне и их круговая эпюра

напряжение от окружного усилия: K = P / F
Для плоских ремней площадь сечения ремня F = bδ
где b — ширина, δ — толщина ремня

Для клиновых ремней F определяется по таблицам ГОСТа.
Напряжение от предварительного натяжения ремня:

Напряжение от усилий натяжения ремня:

Напряжение от действия центробежных сил:  рассматривая сумму проекций сил на горизонтальную ось, получим:

Синус элементарного угла sindα/2 можно принять равным углу в радианах dα/2, тогда центробежная сила элементарного участка ремня, введенного дугой dα:

dN = S_ц sin dα

с другой стороны, элементарная центробежная сила:

Здесь: d_m — элементарная масса выделенного участка ремня;
R — радиус шкива;
ω — угловая скорость вращения шкива;
γ — удельный вес материала ремня;
V — окружная скорость ремня;
g — ускорение силы тяжести

Приравнивая уравнения, получим натяжение ремня от действия центробежной силы:

Напряжение в ремне от действия центробежной силы:

Следует заметить, что напряжение пропорционально квадрату окружной скорости; при малых скоростях оно неве­лико, при больших — резко возрастает.
Напряжение от изгиба ремня:

По закону Гука σ = εЕ

Напряжение изгиба пропорционально толщине ремня, модулю упругости и обратно пропорционально диаметру шкива. Это значит, что отношение D/ρ не должно быть малым (оно указывается в таблицах ГОСТа для каждого типа ремня)

σ_max = σ_ц + σ₁ + σ_u1

Расчет ременных передач до тяговой способности

Плоские ремни:

[K] = [K]_табC_HC_VC_αC_n

[К] — допускаемое расчетное напряжение;
[K]_таб — табличное допускаемое напряжение;
C_H — поправочный коэффициент, зависящий от характера нагрузки;
C_V — поправочный коэффициент, зависящий от скорости ремня;
C_α — поправочный коэффициент, зависящий от угла обхвата ремня;
C_n — поправочный коэффициент, зависящий от расположения передачи.
При горизонтальном расположении C_n = 1

Расчет имеет условный характер и базируется на выборе допускаемых напряжений по кривым скольжения, которые уточняются табличными поправочными коэффициентами

Клиновые ремни:
Число ремней

[Р] = [Р]_табC_HC_VC_αC_n

[Р] — допускаемая расчетная нагрузка на ремень;
[Р]_таб — табличная допускаемая нагрузка