Зубчатые передачи
Достоинства:
практически неограниченная передаваемая мощность
малые габариты и вес
стабильное передаточное отношение
высокий КПД, который составляет в среднем 0,97 — 0,98
Недостатки:
шум в работе на высоких скоростях (может быть снижен при применении зубьев соответствующей геометрической формы и улучшении качества обработки профилей зубьев)
Преимущественное распространение получили передачи с зубьями эвольвентного профиля, которые изготавливаются массовым методом обкатки на зубофрезерных или зубодолбежных станках. Достоинство эвольвентного зацепления состоит в том, что оно мало чувствительно к колебанию межцентрового расстояния
При высоких угловых скоростях вращения рекомендуется применять косозубые шестерни, в которых зубья входят о зацепление плавно, что и обеспечивает относительно бесшумную работу.
Недостатком косозубых шестерен является наличие осевых усилий, которые дополнительно нагружают подшипники. Этот недостаток можно устранить, применив сдвоенные шестерни с равнонаправленными спиралями зубьев или шевронные шестерни.
Шевронные шестерни, ввиду высокой стоимости и трудности изготовления применяются сравнительно редко — лишь для уникальных передач большой мощности.
При малых угловых скоростях вращения применяются конические прямозубые шестерни, при больших — шестерни с круговым зубом, которые в настоящее время заменили конические косозубые шестерни, применяемые ранее.
Конические гипоидные шестерни тоже имеют круговой зуб, однако оси колес в них смещены, что создает особенно плавную и бесшумную работу. Передаточное отнесение в зубчатых парах колеблется в широких пределах, однако обычно оно равно 3 — 5
Основные определения из теории зацепления шестерен
Начальными называются воображаемые окружности, которые при зацеплении шестерен катятся без скольжения одна по другой
Делительными называются воображаемые окружности, по которым происходит номинальное деление зубьев. Для них справедливо уравнение:
d д = mZ
Если шестерни не имеют коррекции, то начальные и делительные окружности совпадают
Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев
Основными называются окружности, по которым развертываются эвольвенты, очерчивающие профили зубьев
d 0 = d д cosα
Шагом t называется расстояние по дуге делительной окружности между одноименными профилями соседних зубьев
Основным шагом t 0 называется шаг по основной окружности
Модулем называется отношение диаметра делительной окружности к числу зубьев или шага к π
Ритчем р называется число зубьев, приходящееся на один дюйм делительной окружности
![]()
Линией зацепления ЛЗ называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении ЛЗ — прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям
Углом зацепления α называется угол между линией зацепления и перпендикуляром к линии центров
Углом наклона спирали зубьев косозубых шестерен β называется угол между осью зуба и образующей делительного цилиндра или конуса
Коэффициентом перекрытия ε называется отношение дуги зацепления к основному шагу
Коэффициентом коррекции ξ называется отношение величины профильного смещения к модулю
Материал и термообработка шестерен
Стальные шестерни изготавливаются из качественных и легированных сталей с термообработкой.
Наибольшее распространение получили: для серийного производства — улучшение; для серийного и массового — цементация и закалка (при наличии соответствующего оборудования — закалка токами высокой частоты)
| Термообработка | Твердость | Материал | Примечания |
| Улучшение (закалка до малой твердости) | НB 260-300 |
Сталь 40 Сталь 45 Cталь 40X Сталь 45Х |
Окончательная нарезка зубьев после термообработки во избежание коробления |
| Закалка | HRC 40-50 |
Сталь 40Х Сталь 40ХН |
Необходима шлифовка зубьев по профилю для устранения коробления |
| Цементация и закалка | HRC 56-63 |
Сталь 20Х Сталь 18ХГТ 12ХНЗА 20ХНЗА 18ХНЗА |
Окончательная обработка зубьев до термообработки. Коробление невелико |
| Закалка ТВЧ | НRC 50-60 |
Сталь 45 Сталь 40Х |
Только для крупных шестерен с модулем > 8 |
Расчетные геометрические зависимости
Прямозубые и косозубые цилиндрические шестерни
Передаточное отношение i :
![]()
Делительные диаметры шестерен:
для прямозубых d д = mZ
для косозубых d д = m sZ = mZ / cos β
Шаг и модуль:
m = t / π; m s = t s / π; t s = t / cos β; m s = m / cos β
Межцентровое расстояние:
для прямозубых
![]()
для косозубых
![]()
Размеры зуба:
h г = f0 m; при f0 = 1, hc = m, hн = 1,25m; hн = 1,25 f0m
по дуге
![]()
где, f 0 — коэффициент высоты зуба; t и m — нормальный шаг и модуль; t s и m s — торцевой шаг и модуль; β — угол спирали зуба
Ряд наиболее распространенных стандартных модулей:
… 1; 1,5; 2; 2,5; 3; 3,5; 4; 4,5; 5; 6; 7; 8; 10; 12 …
Стандартный угол зацепления α — 20°. Для бесшумной и плавной работы косозубых шестерен необходимо перекрытие зубьев: последующий зуб должен входить в зацепление раньше, чем выйдет из зацепления предыдущий
Прямозубые конические шестерни
Все o6paзующие зубьев сходятся в одной точке пересечения осей. Номинальный делительный диаметр, шаг и модуль отсчитываются по большому основанию делительного конуса
Передаточное отношение i:
![]()
Делительный и средний диаметры шестерен:
d д = m Z; d с = m с Z
Конусное расстояние:
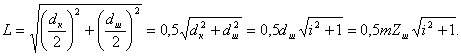
Средний диаметр и модуль:
![]()
![]()
![]()
где, m c — средний модуль;
L — конусное расстояние — длина образующей делительного конуса;
b — ширина зубьев шестерен;
γ — углы конусности
Силы, действующие в зацеплении шестерен
Прямозубые цилиндрические шестерни
Нормальная сила, действующая по линии зацепления, разлагается на две составляющие силы:
P = P ncosα — окружное усилие;
R = P nsinα — радиальное усилие
![]()
![]()
![]()
На валы действуют те же силы, что и на зубья шестерен, и, кроме того, еще крутящий момент:
![]()
Косозубые цилиндрические шестерни
Здесь, вследствие наклона зубьев к образующей, дополнительно возникает еще осевое усилие
окружное усилие
![]()
радиальное усилие:
![]()
осевое усилие:
![]()
нормальное усилие:
![]()
Силы P, R, A необходимо определить для расчета валов и подшипников, сила P n необходима для расчета зубьев шестерен на прочность. Силу A можно уравновесить, применив сдвоенные косозубые шестерни с разнонаправленными спиралями зубьев или шевронные
Конические прямозубые шестерни
Окружное усилие
![]()
Осевое усилие для шестерни или радиальное для колеса: Aш = Rк = R sinγш = P tgα sinγш
Радиальное усилие для шестерни или осевое для колеса: Rш = Aк = R cosγш = P tgα cosγш
Нормальное усилие:
![]()
![]()
![]()
![]()
Силы Р, Aш, Rш — для расчета валов и подшипников, cила Рn — для расчета зубьев на прочность;
dэ, Zэ — диаметры и числа зубьев эквивалентных цилиндрических колес
Воображаемые эквивалентные цилиндрические колеса строятся в плоскости мгновенного зацепления основных конических колес так, что оси тех и других совпадают. Работают эти колеса точно так же, как и основные конические, поэтому такое построение удобно использовать для выяснения действующих сил и напряжений в конических колесах
Дефекты шестерен
Закрытыми называются передачи, заключенные в пыленепроницаемый закрытый корпус, с организованной смазкой.
Открытыми называются передачи, не защищенные от пыли, с нерегулярной смазкой
Износ поверхностей зубьев — очень значительный в открытых передачах и небольшой в закрытых. Меры борьбы с износом — повышение поверхностной твердости зубьев
Питинг — поверхностное выкрашивание зубьев в зоне полосной линии. Возникает вследствие усталости поверхностного слоя зубьев в результате высоких контактных напряжений. Питинг начинается с образования усталостных микротрещин, которые под влиянием циклических нагрузок постепенно развиваются, чему способствует высокое давление масла в зоне контакта зубьев. В открытых передачах питинг обычно не возникает, так как микротрещины изнашиваются раньше, чем успеют развиться.
Меры борьбы с питингом заключаются в повышении жесткости корпусов, валов и опор и точности их изготовления с целью увеличения площадок контакта зубьев
Усталостная изгибная поломка зубьев.
Меры борьбы — увеличение модуля или улучшение качества материала и термообработки
Задиры поверхностей зубьев могут иметь место в тихоходных сильно нагруженных передачах.
Меры борьбы — применение противозадирных смазок, содержащих животные жиры и графит
Расчет зубьев цилиндрических прямозубых шестерен
Расчет на контактную прочность поверхности зубьев
Расчет базируется на известной формуле Герца для контактного сжатия цилиндров с параллельными осями:
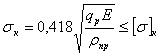
Характерными особенностями контактного сжатия являются:
а) весьма ограниченная площадь контакта я а связи с этим высокие напряжения;
б) объемный характер напряженного состояния;
в) эллиптическая эпюра контактных напряжений, распространяющаяся только на зону контакта
Теоретически интенсивность нагрузки:
![]()
Выразим r м и r к через межцентровое расстояние А:
![]()
![]()
![]()
откуда
![]()
В действительности расчетная интенсивность нагрузки будет отличаться от теоретической на величину поправочных коэффициентов Кк и Кд
![]()
Здесь: Кк — коэффициент концентрации нагрузки, выражающий неполноту контакта по линии. Он зависит от деформации валов и ширины шестерен. Кд — коэффициент динамичности нагрузки, зависящий от окружной скорости и чистоты обработки поверхности зубьев.
Приведенная кривизна зубьев шестерен в точке контакта
![]()
(Знак минус для внутреннего зацепления).
Здесь: ρш и ρк — мгновенные радиусы кривизны в полосе зацепления
![]()
![]()
![]()
Приведенный модуль упругости:
![]()
Здесь: Еш и Ек — модули упругости материала шестерни и колеса.
Если обе шестерни изготовлены из одного материала, то в формулу подставляется:
![]()
Подставляя в основную формулу все величины, получим
![]()
Выразив крутящий момент на оси колеса через мощность в кВт:
![]()
![]()
Получаем проверочную формулу в окончательном виде:
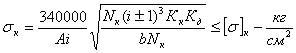
или
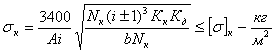
По этой формуле можно проверить и сравнить с допускаемыми, действующие в данной передаче, контактные напряжения.
Для проектного расчета эта формула преобразуется, для чего ширина шестерни выражается через межцентровое расстояние.
Коэффициент относительной ширины
![]() , тогда
, тогда
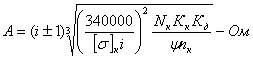
Для редукторов в среднем ψ = 0,2 ÷ 0,4.
Для коробок передач ψ = 0,1 ÷ 0,2.
Здесь: b — ширина шестерни в см;
А — межцентровое расстояние в см;
nк — число оборотов в минуту вала колеса;
N — мощность на валу колеса в кВт;
[σ] — допускаемое контактное напряжение.
По полученной величине межцентрового расстояния можно подобрать модуль, задавшись числом зубьев малой шестерни Zш = 17 — 25 (с коррекцией Z ≥ 14)
![]()
Определение допускаемых контактных напряжений
При циклических нагрузках допускаемые напряжения зависят не только от материала и термообработки, но также и от числа циклов нагружения (времени работы), которое в формуле фигурирует в виде коэффициента режима нагрузки Кр
[σ]к = [σ]таб Кр
где [σ]таб — табличное допускаемое напряжение;
[σ]таб = С1 НВ — для улучшенных сталей;
[σ]таб = С2 HRC — для цементированных и закаленных сталей.
Здесь: С1 и С2 — табличные коэффициенты, зависящие от принятого материала и термообработки.
При постоянном режиме нагрузки:
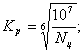 Nц = 60nt – число циклов нагружения
Nц = 60nt – число циклов нагружения
При переменном режиме нагрузки:
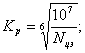
![]()
где Mi, ni, ti — крутящий момент, число оборотов и время работы в часах на каждой ступени усредненного графика нагрузки.
Минимальные значения Кp ограничены наступлением длительного предела выносливости. Для улучшенных сталей Кp ≥ 1, для цементированных и закаленных сталей Кp ≥ 0,59
Расчет на усталостный изгиб зубьев
Опасным нагружением считается такое, которое соответствует моменту начала входа зуба в зацепление. Интенсивность нагрузки q p создает две составляющие, из которых одна сжимает, а другая нагибает зуб.
Опасным сечением считается сечение у корня зуба со стороны растянутых волокон, так как закаленные стальные зубья слабее сопротивляются растяжению, чем сжатию
αl — угол зацепления при вершине зуба
![]()
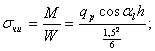
![]()
![]()
Входящие в эти формулы величины S, h и αl аналитически трудно определимы, поэтому формула преобразуется так, чтобы в скобках были безразмерные величины, совокупность которых определяется по таблицам или графикам
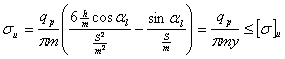
Здесь: y — коэффициент формы зуба; определяется по таблицам или графикам в зависимости от числа зубьев и коэффициента коррекции (если она есть).
Подставив значение q, введенное ране, получаем проверочную формулу:
![]()
Для проектных расчетов формула преобразуется с введением коэффициента относительной модульной ширины шестерни:
![]() обычно Ψм = 6 –10
обычно Ψм = 6 –10
![]()
Выражая величины А и b через модуль, получаем проектную формулу:
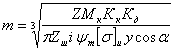
Обычно шестерни закрытых передач рассчитываются на контактную прочность (опасным является питинг) и проверяются на изгиб; шестерни открытых передач, для которых питинг не опасен, рассчитываются только на изгиб
Определение допускаемых напряжений изгиба
Допускаемые напряжения определяются как часть от предела усталости (выносливости) материала при симметричном цикле нагружения
![]() для нереверсивных передач
для нереверсивных передач
![]() для реверсивных передач
для реверсивных передач
Здесь: n1 — коэффициент запаса прочности по пределу усталости, Кσ — коэффициент концентрации напряжений у ножки зуба, Kрн — коэффициент режима нагрузки по изгибу, можно принимать его равным 1 для большинства передач (только для очень тихоходных передач он может быть больше единицы)
Особенности расчета косозубых цилиндрических шестерен
Принципиально расчетные формулы для косозубых шестерен те же, что и для прямозубых, отличие заключается в следующем:
| Оценочный параметр | Прямозубые | Косозубые |
| Нагрузка на зуб | ||
| Длина контактных линий |
Особенности расчета конических прямозубых шестерен
Конические шестерни рассчитываются как эквивалентные им цилиндрические.
Окружное усилие определяется по среднему диаметру, расчетным является средний модуль. При определении коэффициента формы зуба принимается эквивалентное число зубьев
![]()
Коррекция зубьев шестерен
В целях уменьшения габаритов и веса машин желательно у малых шестерен число зубьев делать минимальным, однако этому препятствует подрез ножки зуба, который для эвольвентного двадцатиградусного зацепления имеет место при Z < 17 зубьев. Вводя коррекцию (теоретическое исправление профиля), можно уменьшить Zmin до 14 зубьев и даже менее
Угловая коррекция (фау-коррекция) заключается в смещении профиля зубьев малой шестерни в плюс (от центра) на величину:
V = ξ m
где ξ — коэффициент коррекции
При этом увеличивается на величину V межцентровое расстояние, а также угол зацепления, так как при раздвижке центров раздвигаются соответственно и основные окружности, к которым касательна линия зацепления
Высотная коррекция (фау-нуль-коррекция), при которой профиль зубьев малой шестерни смещается в плюс (+V), а профиль зубьев колеса на столько же — в минус (-V). При этом межцентровое расстояние и угол зацепление не меняются, изменяются лишь относительная высота головки и ножки зубьев.
Изготовление корригированных шестерен не представляет никаких трудностей
КПД зубчатых передач
Для закрытых передач в среднем:
цилиндрических η =0,98
конических η = 0,97
Для открытых передач:
цилиндрических η = 0,97
конических η = 0,96
Эти цифры включают также потери в опорах качения, которые невелики и составляют от 0,25 до 0,5 % на опору при надежной смазке
Смотри также:
- Муфта фрикционная сухого трения
- Комбинированная двухконусная фрикционная предохранительная муфта
- Подбор и расчет валов
- Как определить и обозначить шероховатость поверхности
- Расчет соединений с гарантированным натягом
- Червячные передачи
- Ременные передачи
- Цепные передачи
- Фрикционные передачи
- Шпоночные соединения
- Расчет шлицевых соединений