Расчет подшипников скольжения

Критерии расчетов подшипников скольжения зависят прежде всего от характера трения в подшипнике. Можно выделить три основных вида трения скольжения: граничное, смешанное (или полужидкостное) и жидкостное.

Граничное трение имеет место при небольших скоростях скольжения трущихся поверхностей, при этом толщина слоя смазки порядка 0,1 мкм. Можно считать, что в этих условиях коэффициент трения имеет постоянную величину и сила трения определяется законом Амонтона — Кулона

T = f N, (1)
где Т – сила трения;
f — коэффициент трения;
N – нормальная сила

С увеличением скорости скольжения v = ωr величина f уменьшается, становясь весьма неустойчивой в связи с тем, что трение переходит в смешанное, при котором, несмотря на увеличившуюся толщину слоя смазки, все еще имеет место соприкосновение отдельных выступов трущихся поверхностей.

Минимальное значение коэффициента трения f_min соответствует границе перехода к жидкостному трению, при котором трущиеся поверхности полностью разделены слоем смазки. Режим жидкостного трения наступает при определенном сочетании следующих величин: динамической вязкости масла µ, угловой скорости ω, относительного диаметрального зазора в подшипнике ψ = ∆/d (∆ — диаметральный зазор) и среднего давления р = P/ld (здесь Р — радиальная нагрузка подшипника, d и l — диаметр и длина цапфы)

Для подшипников, работающих в условиях граничного или смешанного трения, производят упрощенные расчеты по двум критериям: среднему давлению p и произведению pv.
Расчет подшипников жидкостного трения основан на гидродинамической теории смазки.
Условная граница, отделяющая режим жидкостного от режима полужидкостного трения, определяется с помощью критических значений безразмерных чисел Зоммерфельда [S₀] = pψ²/µω. При pψ²/µω ≥ [S₀] — трение полужидкостное,  пpи pψ²/µω; [S₀] — трение жидкостное.

Для случаев, когда чистота трущихся поверхностей соответствует Ra 0,4, прогиб шипа в подшипнике не превышает сумму высот неровностей и погрешности формы не превосходят половины допуска диаметра, приведена таблица 1 критических значений [S₀], при которых минимальная толщина слоя смазки h_min = 10 ÷ 15 мкм. С помощью чисел [S₀] можно определить критические значения скоростей v₂, при превышении которых наступает жидкостное трение:

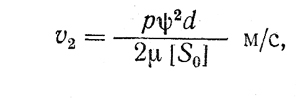
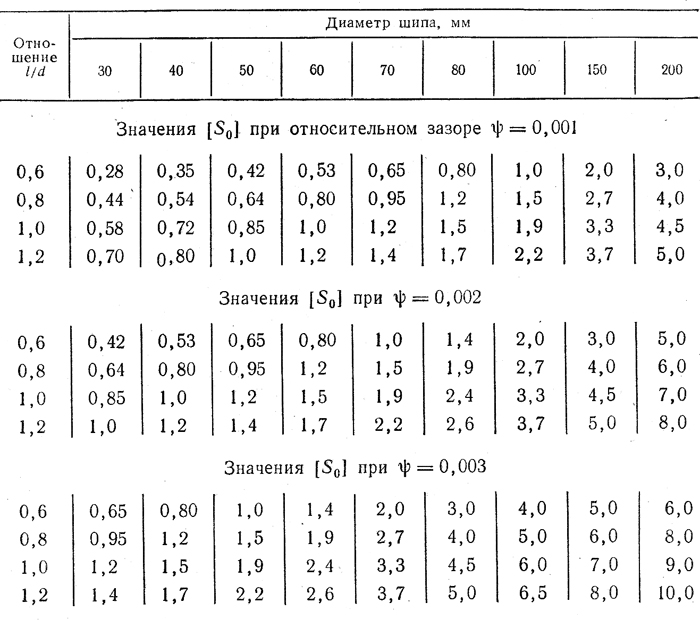
Значения [S₀], соответствующие условной границе между полужидкостным и жидкостным трением (при pψ²/µω < [S₀] — трение жидкостное, пpи pψ²/µω > [S₀] — трение полужидкостное

Таблица 1

Упрощенный расчет подшипников скольжения

Расчет основан на удовлетворении условий:
1) р≤[p] и 2) pv≤lpv], (3)
где р = P/ld — среднее давление в подшипнике;
Р — радиальная нагрузка на подшипник, Н;
d — диаметр цапфы, мм;
l — длина цапфы, мм;
v — скорость скольжения, м/с.

Первое условие отражает требования к износостойкости подшипника.
Величина pv в какой-то мере отражает тепловую напряженность подшипникового узла и поэтому может служить условным критерием расчета на ограничение нагрева трущихся поверхностей.
Величины p и pv лишь приближенно характеризуют напряженность работы подшипника, поскольку они не отражают влияния ряда важнейших факторов на работоспособность узла: первоначального зазора и чистоты поверхности, степени изношенности подшипника и др.

Приводимые в различных источниках значения [p] и [pv] представляют собой средние статистические данные, относящиеся к определенным конструкциям.

В табл. 2 приведены значения [p] и [pv] для подшипников с чугунными и бронзовыми вкладышами (меньшие значения для чугунных вкладышей, большие — для бронзовых).
Применительно к различным материалам подшипников скольжения в таблицах 3; 4; 5; 6 и 7 даны значения [p], [pv] и [v]. Коэффициент трения — по таблице 8

Таблица 2
Величины [р] и [pv] для некоторых узлов машин

Область применения	[р], Н/мм2	[pv], Нм/мм2с
Редукторы	2 — 6	4 — 8
Электродвигатели	1,0 — 3	4 — 10
Подшипники промежуточных валов приводов транспортеров и конвейеров	2 — 5	3 — 8

Таблица 3
Антифрикционный чугун для подшипников скольжения (по ГОСТу 1585—85) и серый чугун (по ГОСТу 1412—85)

Марка	Твердость, НВ	[р], Н/мм2	[v], м/с	[pv], Нм/мм2с
АЧС-1	180-229	0,05	2	0,1
АЧС-1	180-220	9	0,2	1,8
АЧС-2	190-229	0,1	3	0,3
АЧС-3	160-100	1,0	0,75	4,5
АЧВ-1	210-260	0,5	5	2,5
АЧВ-2	167-197	12	1,0	12,0
АКЧ-1	197-217	0,5	5	2,5
АКЧ-2	167-197	12	1,0	12,0
Серый чугун СЧ 15; СЧ 18; СЧ 25		4 при 0,5 и продолжительных интервалах в работе 2 при 1 0,1 при 2

Примечания: 1. Для промежуточных значений v величина [pv] определяется интерполированием.
2. Подшипники из чугуна АЧС-1, АЧС-2, АЧВ-1, АКЧ-1 предназначены для работы с закаленным или нормализованным валом, из АЧС-3, АЧВ-2, АКЧ-2 — с незакаленным валом.
Бронза и латунь для подшипников скольжения
Таблица 4

Марка	Область применения	[р], Н/мм2	[v], м/с	[pv], Нм/мм2с
Бр.ОФ10-1 Бр.ОФ6,5-0,15 Бр.ОЦС5-5-5 Бр.ОЦС6-6-3 Бр.ОЦС4-4-17	Подшипники паровых турбин, генераторов и электродвигателей, центробежных насосов и компрессоров	15 — 8 5 10	10 — 3 3 4	15 — 12 10 10
Бр.АЖ9-4 Бр.АЖ9-4Л Бр.АЖМц10-3-1,5 Бр.АЖС7-1,5-1,5	Подшипники центробежных насосов и компрессоров, электродвигателей, металлорежущих станков, редукторов, прокатных станов	15 — 20 25	4 — 5 8	12 — 12 20
ЛМцОС58-2-2-2 ЛКС80-3-3 ЛМцЖ52-4-1	Подшипники транспортеров, кранов, рольгангов, редукторов, вибраторов, экскаваторов, дробилок	10 12 4	1 2 2	10 10 6

Баббиты и их заменители
Таблица 5

Марка	Область применения	[р], Н/мм2	[v], м/с	[pv], Нм/мм2с
Б89; Б83	Подшипники, несущие большую нагрузку и работающие при большой скорости скольжения: паровых турбин, турбогенераторов, электродвигателей мощностью свыше 750 кВт, двигателей внутреннего сгорания	20	60	15
Б16	Подшипники электродвигателей, тракторов, центробежных насосов и компрессоров, прокатных станов и других машин, работающих без резких изменений нагрузки	15	12	10
Б6	Подшипники редукторов, насосов, вентиляторов, лебедок, шаровых мельниц, небольших прокатных станов и других машин, работающих с умеренной нагрузкой без резких ударов	5	6	5
БН	Подшипники паровых турбин и электродвигателей средней мощности, автотракторных двигателей, поршневых компрессоров и других машин, работающих с переменной и ударной нагрузкой	20	15	15
БК; БК2	Подшипники, воспринимающие ударные нагрузки: тихоходных двигателей внутреннего сгорания, прокатных станов, металлорежущих станков, буксы вагонов	15	15	6
Заменители: ЦАМ10-5; ЦАМ10-1,5 (сплавы цинка, алюминия, меди)	Подшипники машин работающих с умеренной нагрузкой без резких ударов	12	10	12

Металлокерамические подшипники ([р], Н/мм²)
Таблица 6

Материал	Пористость, %	0,1 v, м/с	0,2 v, м/с	1 v, м/с	2 v, м/с	3 v, м/с	4 v, м/с
Бронзографит 9-10%, Sn 1-4% графита, остальное Cu	15-20	18	7	6	5	3,5	1,2
Бронзографит 9-10%, Sn 1-4% графита, остальное Cu	20-25	15	6	5	4	3	1
Бронзографит 9-10%, Sn 1-4% графита, остальное Cu	25-30	12	5	4	3	2,5	0,8
Железографит 1-3% графита, остальное Fe	15-20	25	8,5	8	6,5	4,5	1
Железографит 1-3% графита, остальное Fe	20-25	20	7	6,5	5,5	3,5	0,8
Железографит 1-3% графита, остальное Fe	25-30	15	5	5	4	2,5	0,6

Прочие материалы
Таблица 7

Марка	Свойства и область применения	[р], Н/мм2	[v], м/с	[pv], Нм/мм2с
Графитовые втулки	Стойки в агрессивных средах и в диапазоне температур от 100 до 600° С	до 1,5	до 1	—
Графитовые втулки, пропитанные свинцом или баббитом при смазке минеральным маслом	Легко нагруженные опоры	до 10	≤ 1	—
Пластографит (антегмит), получаемый на основе графита с фенолформальдегидной смолой	Легко нагруженные опоры	—	—	—
Текстолит при смазке водой	Применяется в виде плит для наборных вкладышей и в виде крошки для прессованных вкладышей. Имеет низкую теплопроводность и высокий коэффициент трения (0,124-0,15) при работе без смазки	30	≤ 1	25
Текстолит при смазке маслом	Применяется в виде плит для наборных вкладышей и в виде крошки для прессованных вкладышей. Имеет низкую теплопроводность и высокий коэффициент трения (0,124-0,15) при работе без смазки	—	≤ 6	20
Капрон АК-7 и 68 при смазке маслом	Применяется для нанесения тонкого слоя на рабочую поверхность вкладыша или в виде тонкостенных вкладышей. Имеют низкий коэффициент теплопроводности, поглощают воду, нестабильны в размерах	≤ 15	≤ 4	15-20
Полиамиды 54 и 548	Применяется для нанесения тонкого слоя на рабочую поверхность вкладыша или в виде тонкостенных вкладышей. Имеют низкий коэффициент теплопроводности, поглощают воду, нестабильны в размерах	≤ 7,5	—	7,5-10
Поликарбонат	По антифрикционным свойствам близок к АК-7. Устойчив в маслах, бензине, слабых кислотах, но разрушается в щелочах. Водопоглощение меньше, чем у полиамидов	—	—	—
Политетрафторэтилен (фторопласт)	Имеет низкие механические качества. Применяется для нанесения покрытий на поверхностях скольжения и для пропитки пористых вкладышей	—	—	0,35
Пластифицированная древесина	Применяется для наборных вкладышей подшипников, несущих умеренную нагрузку и смазываемых водой	10	≤ 1	—
Лигнофоль	Для изготовления прессованных вкладышей, смазка водой	≤ 6	—	—
Древеснослойные пластинки (ДСП)	Для наборных вкладышей, смазываемых водой (в гидротурбинах, насосах, прокатных станках)	≤ 35	≤ 8	≤ 35
Резина	Применяется в виде цельных вкладышей или для облицовки крупных подшипников, смазываемых водой	≤ 2	—	—
Резина твердая вулканизированная	Применяется в виде цельных вкладышей или для облицовки крупных подшипников, смазываемых водой	до 6	—	—

Значения коэффициента трения f при граничном трении для стального вала по подшипникам из различных материалов
Таблица 8

Материал подшипника	f
Серый чугун	0,15—0,20
Антифрикционный чугун	0,12—0,15
Бронза	0,10—0,15
Баббитовая заливка	0,07—0,12
Сплав АСМ	0,10—0,15
Текстолит	0,15—0,25
Полиамиды (капрон и др.)	0,15—0,20
Дерево	0,20—0,30
Пластифицированная древесина и древеснослоистые пластики	0,15—0,25
Бронзографит	0,08—0,12
Железографит	0,10—0,15
Сталь со слоем MoS2	0,08—0,15
Металлический вкладыш со слоем фторопласта	0,04—0,08

Момент сил трения в подшипнике

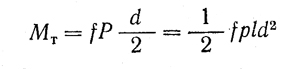
Тепловыделение в подшипнике
W = Mтω = fPv (5)
Величины f и v в эту формулу следует подставлять с учетом режима работы подшипника в соответствии с табличными данными

Скорость v₁ при которой начинается переход от граничного трения к полужидкостному, определяется из формулы Фогельполя

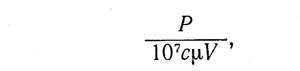
где Р — нагрузка на подшипник, Н;
µ — динамическая вязкость масла, Н•с/м²;
V = πd²l/4рабочий объем подшипника, м³;
с — постоянный коэффициент, назначаемый по следующим рекомендациям:
Серый чугун с = 1 ÷ 2
Антифрикционный чугун с = 1,5 ÷ 2,5
Бронза с = 2 ÷ 3
Баббит с = 2,5÷ 4
(Большие значения — для самоустанавливающихся подшипников)
Заменив в формуле  Фогельполя P/ld = p,  получим

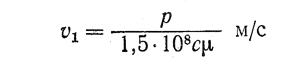
Коэффициент трения определяется по формуле

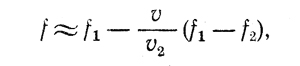
где v — скорость скольжения;
v₂ — скорость скольжения, соответствующая границе перехода из режима полужидкостного трения в жидкостное и определяемая по формуле (1);
f₂— коэффициент трения, соответствующий v₂.
Величина f₂ определяется по формуле Фальца

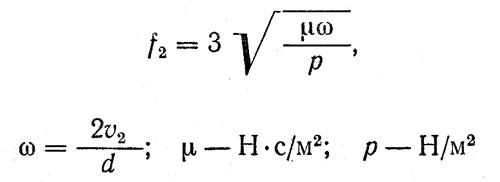
Расчет подшипников жидкостного трения

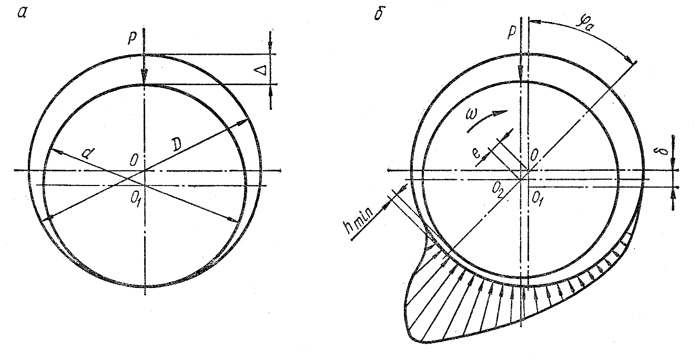
рис. 1
Положение шипа в подшипнике: а — в состоянии покоя; 6 — при вращении со скоростью)
На рисунке 1 показаны схемы расположения шипа в подшипнике: в начале его работы (рис. 1, а), когда угловая скорость шипа ω еще близка к нулю, и в период установившегося движения, когда угловая скорость ω становится больше критического значения, соответствующего переходу в режим жидкостного трения (рис. 1, 6).

В случае, изображенном на схеме рис. 1, а, центр O₁ шипа лежит на линии действия внешней силы Р на подшипник под его центром О, при этом эксцентриситет e=OO₁ равен радиальному зазору в подшипнике δ, т. е. е = δ = ∆/2.

В положении шипа по схеме 1, б центр шипа занимает новое положение О₂ Минимальная толщина масляного слоя h_min находится на линии центров ОО₂, и равна
h_min = δ – е = δ(1-χ) (10)
где χ = е/δ – относительный эксцентриситет.

При изменении угловой скорости центр шипа соответственно меняет свое положение; траектория его движения в подшипнике приближенно дуга окружности. При ω → ∞ трущиеся цилиндрические поверхности шипа и подшипника становятся почти концентрическими, образуя постоянный по окружности кольцевой зазор, равный δ.

Угол φ_а между линией центров шипа и подшипника и линией действия нагрузки Р, а также эксцентриситет е полностью определяет положение шипа в подшипнике.

Развивающиеся в клиновом масляном зазоре гидродинамические силы распределены по закону, изображенному на схеме рис. 1, б. Эти силы уравновешивают нагрузку Р на шип. Определение несущей силы Р масляного слоя в подшипнике является одной из задач гидродинамической теории смазки.
Поскольку условия образования несущего масляного слоя в подшипнике аналогичны гидродинамическим процессам, возникающим между плоскостью и перемещающейся под некоторым углом к ней пластиной, то в основу гидродинамического расчета радиальных подшипников может быть положено следующее уравнение Рейнольдса для плоского потока жидкости, определяющее изменение давления в нем при бесконечно большой ширине потока в направлении, перпендикулярном направлению скорости v движения пластины:

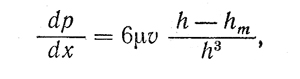
где µ — вязкость масла, Н•с/м²;
h_m — зазор в сечении максимума давления, мм;
к — зазор в произвольном сечении с координатой х, мм;
v — скорость, м/с.
Применительно к радиальному подшипнику это уравнение (12) записывают в полярных координатах

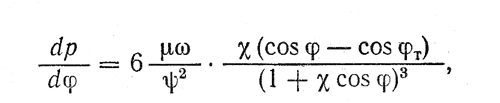
где p — давление в произвольном сечении под углом φ к линии центров;
µ — динамическая вязкость;
ψ = ∆/d – относительный зазор;
χ = е/δ – относительный эксцентриситет;
δ – радиальный зазор.
Угол φ_т соответствует сечению с p_max.
Уравнение (12) после интегрирования и ряда преобразований приводится к формуле 13 для определения гидродинамической грузоподъемности подшипника

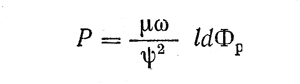
где Ф_р — коэффициент напряженности, являющийся безразмерной функцией положения цапфы в подшипнике и границ зоны несущего слоя смазки, зависящей также от отношения l/d.
Функция Ф_р вычисляется обычно графическим интегрированием для границ несущей зоны, начинающейся от места ввода смазки и кончающейся сечением с р = 0 и d_p/d_φ = 0.
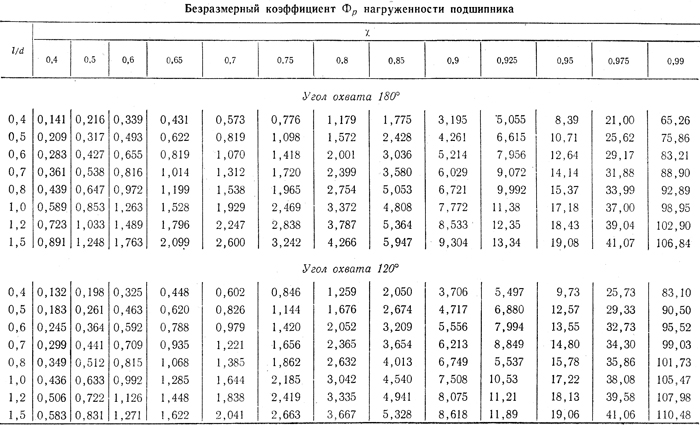
Величины Ф_р с учетом конечной длины подшипника для указанных границ несущей зоны в подшипниках с углами охвата 180° и 120° приведены в табл.9.
Величины, входящие в формулу (13), должны быть подставлены в следующих единицах: Р — Н; µ— Н • с/м²; ω — в рад/с; l и d — м

Таблица 9

При гидродинамическом расчете подшипника обычно известны: нагрузка Р, угловая скорость ω и размеры подшипника d и l, предварительно определенные расчетом вала. Величина ψ определяется выбранной посадкой шипа в подшипнике (H7/f7 или H9/f9) и обычно находится в пределах ψ = 0,001 ÷ 0,003. Вязкость масла можно предварительно определить на основании данных табл.1, используя условие

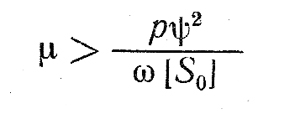
Из формулы 13 выводится величина Ф_р

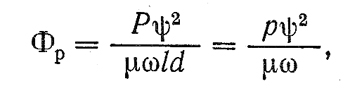
по которой затем из табл. 9 определяется по известному отношению l/d значение χ. Далее находят величину h_min = δ(1-χ),

которую сравнивают с величиной ∑R_z + y_о, где ∑R_z — сумма высот неровностей поверхностей шипа и подшипника для выбранного класса их чистоты по ГОСТу 2789—73; у₀— прогиб шипа в подшипнике; для двухопорного вала = 1,6y₀(l/L)y_max, причем y_max – стрела прогиба вала на участке между опорами, a L — расстояние между серединами опор; в остальных случаях величина уо определяется при расчете вала.

Класс чистоты рабочих поверхностей шипа и подшипника назначается в зависимости от величины ψ и χ; класс чистоты должен быть тем выше, чем меньше эти величины. Должно соблюдаться условие
h_min > 1,1(∑R_z + y_о) (16)

где коэффициент 1,1 есть запас, учитывающий влияние возможных случайных факторов. Кроме того, необходимо учитывать погрешности формы, если они выходят за пределы допуска размера

Сопротивление слоя смазки вращению шипа

Силы вязкости смазывающей жидкости оказывают сопротивление вращению шипа и вызывают потери на трение в подшипнике. Считая, что весь зазор в подшипнике полностью заполнен маслом, удельное сопротивление вращению шипа в подшипнике определяют по закону Ньютона для вязкой несжимаемой жидкости

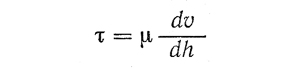
и далее находят полную силу трения на поверхности s подшипника

Из этого выражения путем использования тех же допущений, которые были приняты при определении гидродинамической грузоподъемности подшипника, получают формулу для определения силы сопротивления в подшипнике

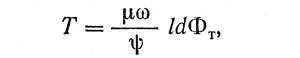
где Ф_т — характеристика трения, представляющая собой безразмерную функцию положения шипа в подшипнике, границ несущего слоя и отношения l/d.
Коэффициент трения в подшипнике определяется следующим образом

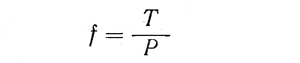
или с учетом выражений для Т и Р

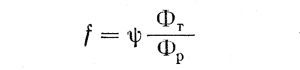
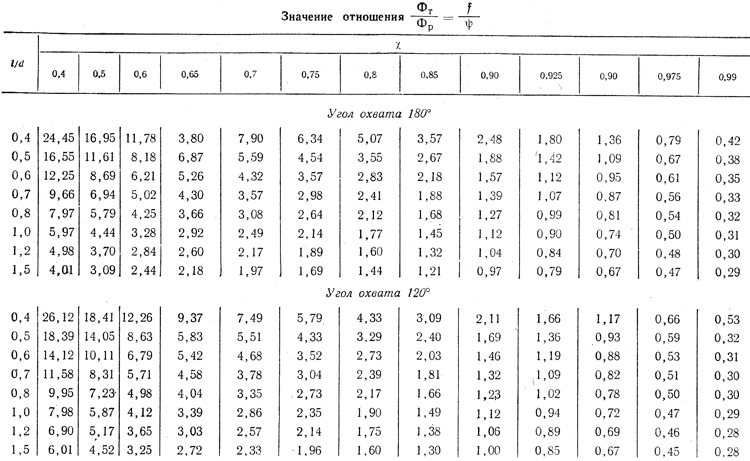
В таблице 10 приводятся значения отношений Ф_т/Ф_р
Таблица 10

Тепловыделение в подшипнике (формула 21)

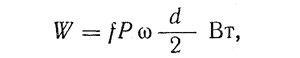
где d — в м; Р — в Н; ω— в рад/с

Тепловой расчет подшипника

Для составления теплового баланса подшипника необходимо знать, какое количество масла протекает через подшипник в единицу времени, т. е. расход смазки. Кроме того, знание расхода масла необходимо для расчета смазочной системы.

Полный расход смазки определяется истечением через торцы в нагруженной зоне, в ненагруженной зоне и через канавки для смазки.

Секундный расход смазки через торцы подшипника

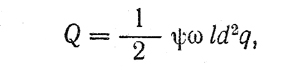
где q — безразмерный коэффициент
q = q₁ +q₂ + q₃
В этой формуле: q₁ — коэффициент расхода смазки через торцы нагруженной зоны, определяемый по табл. 11

Таблица 11

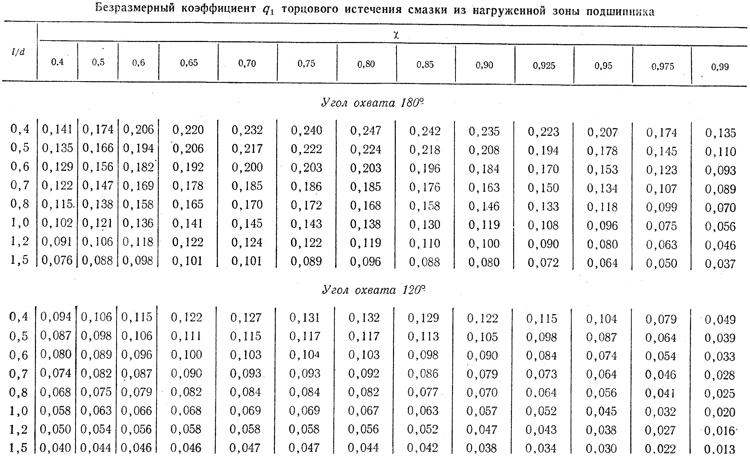
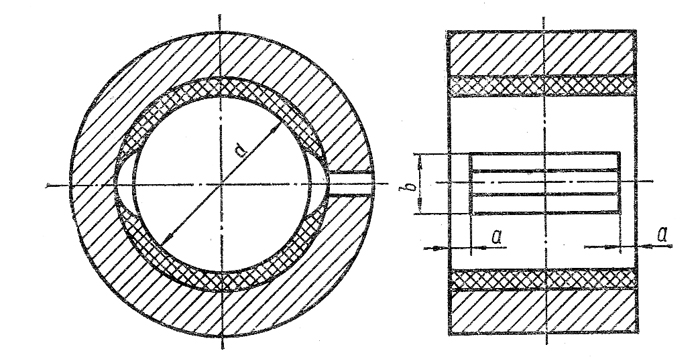
Рис 2    Смазочные канавки в подшипнике

q₂ — коэффициент расхода смазки через торцы ненагруженной зоны;
q₃ — коэффициент, учитывающий истечение через канавки для смазки. При двух канавках в плоскости разъема подшипника (рис. 2)

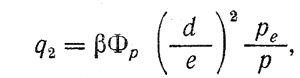
где р_е — давление принудительной подачи смазки в подшипник;
p = P/ld — среднее давление;
β — безразмерный коэффициент, определяемый по таблице 12

Таблица 12

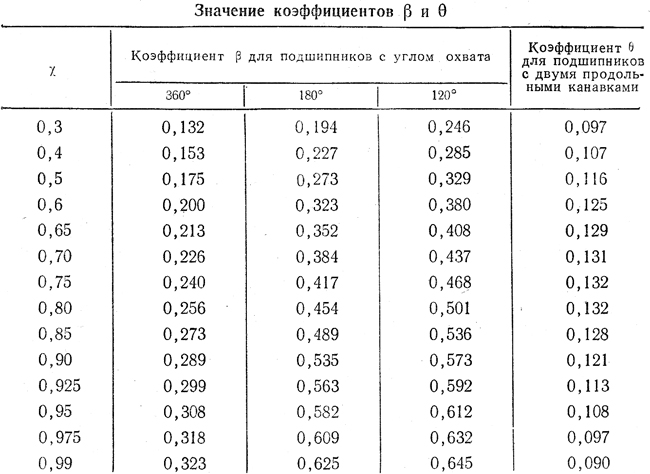
Коэффициент q₃ определяется по формуле

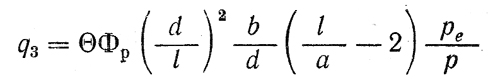
где Θ — безразмерный коэффициент, определяемый по таблице 12
Размеры a и b рекомендуется определять по формулам: a ≈ 0,05d + (3 ÷ 5) мм; b ≈ (0,20 ÷ 0,25)d

Количество тепла, переносимого смазкой,
W₁ = cQ(t₂ — t₁) Вт, (25)
где с — удельная объемная теплоемкость масла, Дж/м³ • град;
Q — расход масла, м³/с;
t₁ и t₂ — температура смазки на входе и выходе из подшипника

Количество тепла, отводимого корпусом подшипника во внешнюю среду,
W₂ = kF (t_м — t_в) Вт, (26)
где k — коэффициент теплопередачи, Вт/м² град;
F — поверхность подшипника, омываемая воздухом, м²;
t_М — средняя температура масла в нагруженной зоне;
t_B — температура окружающего воздуха.
Средние значения k лежат в пределах 9 ÷ 16 Вт/м² град
Уравнение теплового баланса при установившемся режиме работы подшипника
W = W₁ + W₂, (27)
где W — по формуле (21)

Поскольку температура масла в нагруженной зоне подшипника заранее не известна, то, задаваясь значениями средней температуры смазки, можно вести гидродинамический расчет подшипника методом последовательных приближений.

Точно так же методом последовательных приближений приходится решать задачи по определению оптимальных значений ψ или вязкости масла µ, приводя каждое решение к удовлетворению условия (27)

Упорные подшипники (подпятники)

Геометрические особенности простейших подпятников (рис. 3) таковы, что в них нет условий для образования масляного клина между трущимися поверхностями, поэтому они работают в режимах граничного или полужидкостного трения

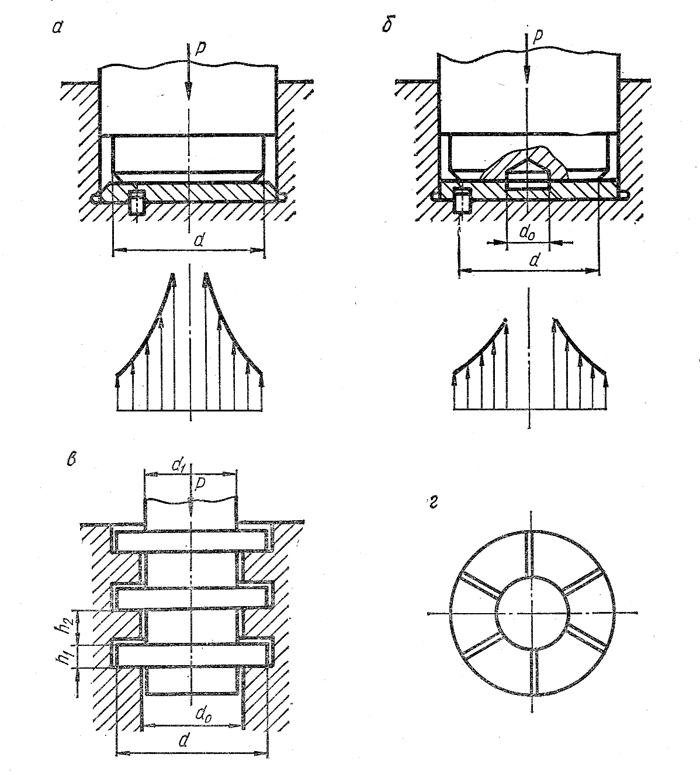
рис. 3 Схемы упорных подшипников: а) сплошная пята; б) кольцевая пята; в, г) гребенчатая пята;

Смазочные канавки на опорной поверхности подпятника (рис. 3, г) облегчают попадание смазки в зону трения. Расчеты подпятников проводят по условиям:

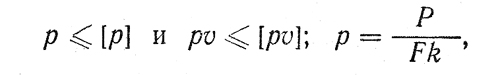
где Р — осевая нагрузка, Н
F — опорная поверхность, мм²
k ≈ 0,8 — 0,9 — коэффициент, учитывающий уменьшение опорной поверхности из-за смазочных канавок. Нормы для [р] и [pv] примерно такие же, как и для радиальных подшипников скольжения.
Площадь опорной поверхности F = πd²/4 — для сплошной пяты; F = π/4(d² — d²₀) — для кольцевой, где d₀ = (0,6 — 0,8)d
Допустив, что р = const, определяем момент трения на кольцевой пяте

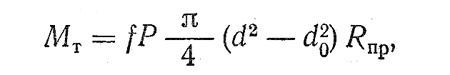
где приведенный радиус трения

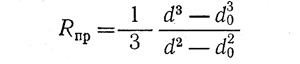
Для сплошной пяты R_пр = 1/3d
Скорость скольжения определяют ни приведенном радиусе

Число гребней в гребенчатой пяте (рис. 3, в) определяют по соотношению

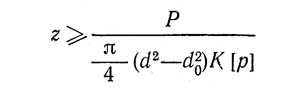
Для гребенчатой пяты величины [p] и [рv] принимают с учетом неравномерного распределения нагрузки по гребням на 20 — 40% меньше, чем для радиальных подшипников.